当一束光从焦点发射，并在与圆锥曲线相交的点处发生反射时，反射的光线必定：

• 穿过另一焦点（椭圆）；

  

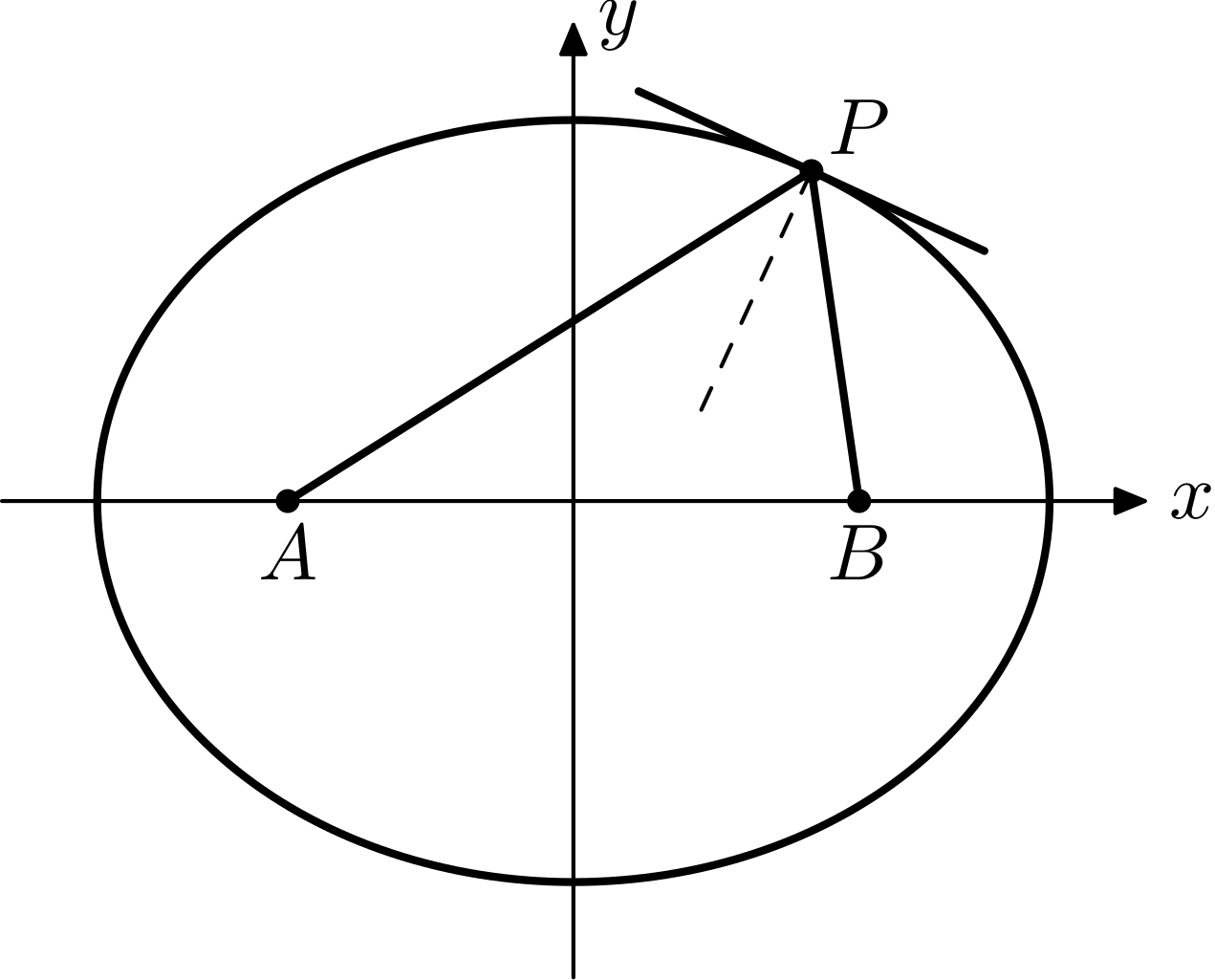
• 反向延长后穿过另一焦点（双曲线）；

  

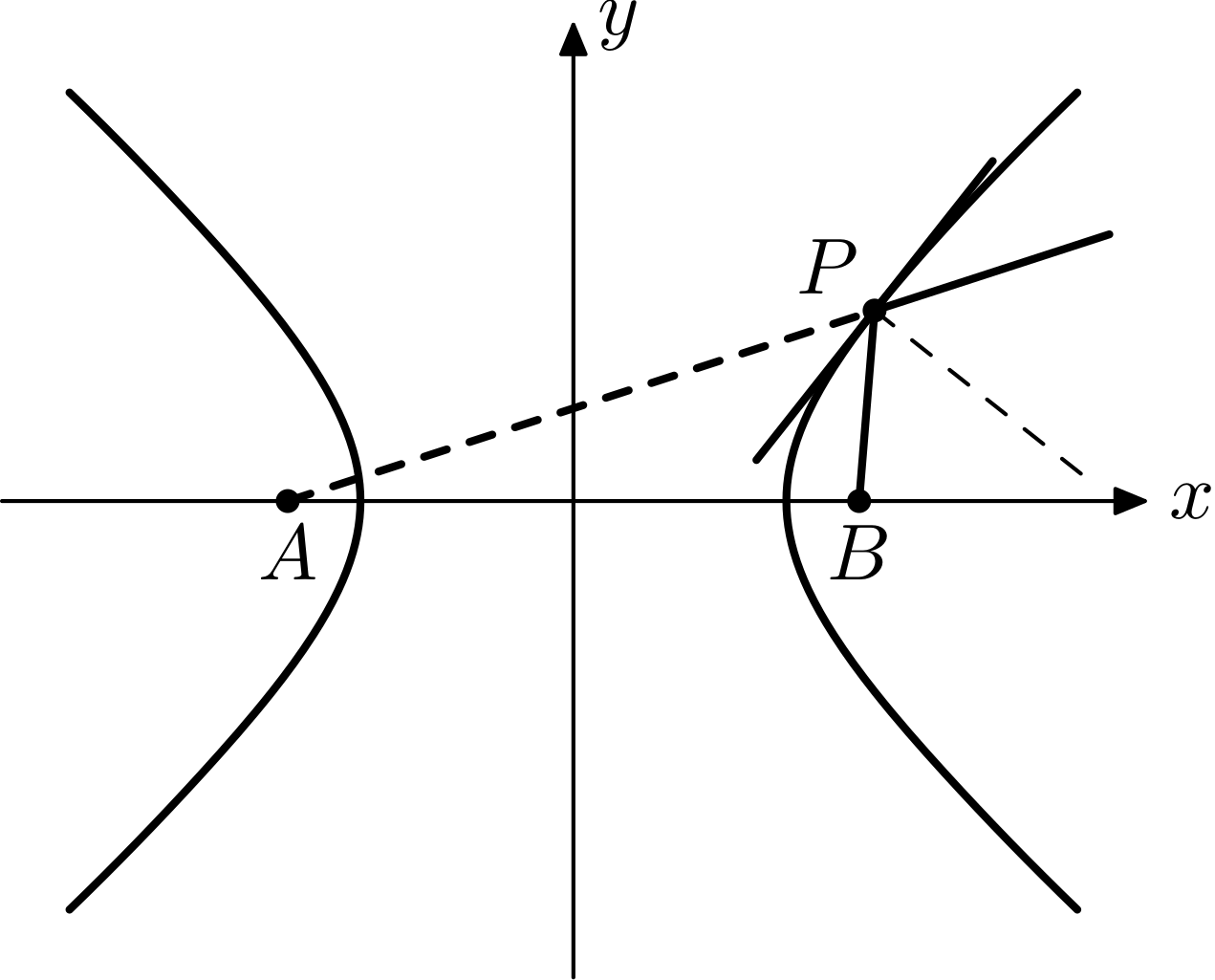
• 与对称轴平行（抛物线）。这个性质使得它的旋转曲面很适合用来发出/收集平行光。

  

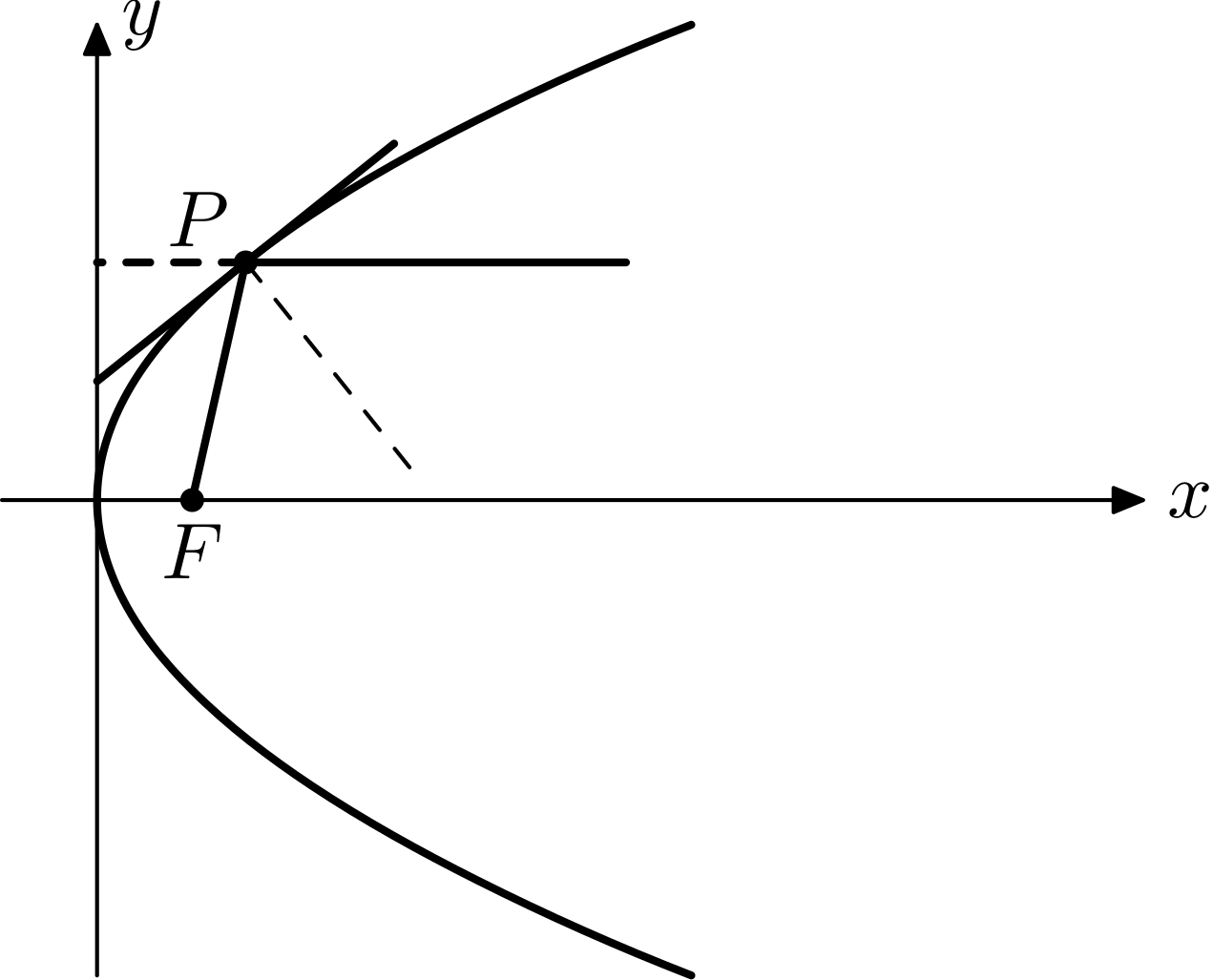
证明的办法：先在曲线上任取一点P，作焦点和P的连线（如果是抛物线则另作一条过P且与对称轴平行的线），然后证明所作的线与法线（或切线）构成的锐（直）角相等即可。

以椭圆为例， 不失一般性， 设椭圆方程为 \[{x^2\over a^2}+{y^2\over b^2}=1\qquad(a>b>0).\] 则椭圆上的点可以用\(P(a\cos\theta, b\sin\theta)\)表示，而焦点为\(F_\pm(\pm c, 0)\)，其中\(c=\sqrt{a^2-b^2}\)。 \[\eqalign{ |\overrightarrow{F_\pm P}| &= \sqrt{a^2\cos^2\theta \pm 2ac\cos\theta + c^2 + b^2\sin^2\theta}\cr &= \sqrt{a^2 \pm 2ac\cos\theta + c^2\cos^2\theta}\cr &= a \pm c\cos\theta.\cr }\]

切向量可以通过对\(\overrightarrow{OP}\)求关于参数\(\theta\)的导数得到： \[\vec t = (-a\sin\theta, b\cos\theta).\]

由平面向量夹角公式， \[\eqalign{ \cos\langle\overrightarrow{F_\pm P},\vec t\rangle &= {\overrightarrow{F_\pm P}\cdot\vec t \over |\overrightarrow{F_\pm P}| |\vec t|}\cr &= {-a\sin\theta(a\cos\theta\pm c)+b^2\sin\theta\cos\theta \over (a\pm c\cos\theta)|\vec t|}\cr &= {-c\sin\theta(\pm a + c\cos\theta) \over (a\pm c\cos\theta)|\vec t|}\cr &= {\mp c\sin\theta \over |\vec t|}\cr }\] 绝对值相等，这说明\(\overrightarrow{F_\pm P}\)与切线构成的锐（直）角相等。证毕。

对于双曲线，可设其方程为 \[{x^2\over a^2}-{y^2\over b^2}=1\qquad(a>0,\,b>0).\] 双曲线位于\(y\)轴右侧一支上的点可用\(P(a\sec x, b\tan x)\)表示，而焦点为\((\pm c, 0)\)，其中\(c=\sqrt{a^2+b^2}\)。

进行类似计算可知所构成的锐（直）角也相等。

对于抛物线，可设其方程为 \[y^2 = 4cx\qquad(c>0).\] 其上的点可用\(P(4ct^2, 4ct)\)表示，而焦点为\(F(c, 0)\)。

\[\eqalign{ |\overrightarrow{FP}| &=\sqrt{(4ct^2-c)^2+(4ct)^2}\cr &=(4t^2+1)c\cr }\]

切向量（约去常数\(4c\)） \[\vec t=(2t, 1)\]

因此 \[\eqalign{ \cos\langle\overrightarrow{FP},\vec t\rangle &={(4ct^2-c)(2t) + (4ct) \over (4t^2+1)c|\vec t|}\cr &={2t\over |\vec t|}\cr }\]

与对称轴平行的向量\(\vec x=(1, 0)\)， \[\eqalign{ \cos\langle\vec x,\vec t\rangle &={2t\over |\vec t|}\cr }\]

由此可知所作的两条线与切线所构成的锐（直）角相等。

附：图的画法