Golang Project页面右侧有一张图片：

一只gopher拿着游标卡尺，工程师的经典工具。另一只gopher拿的东西现在很少见了，叫做计算尺(slide rule)。它曾经也是科学技术人员必备的工具，可以不打草稿进行乘除运算，常见的有3位有效数字，能满足一般的工程需要。

自从1972年手持式科学计算器HP-35面市，计算尺迅速被淘汰。科学计算器运算速度快、精度高、功能丰富，各方面指标完胜已有的计算工具。现在已经没有厂家生产计算尺；它已成为一种收藏品。

另一个同样被淘汰的工具是算盘。这个工具在中国非常流行。有意思的是，算盘是数字式的，它本身只能处理离散值，不存在失真的问题，精度高。相比之下计算尺是模拟式的，理论上有无限的精度，但是因为存在加工精度限制、装配误差等，实际上精度并不高。电子计算器普及后，算盘也被淘汰了。耐人寻味的是，现在仍然有厂家生产算盘。

这里还要提一个因科学计算器普及而变得过时的技术：常用对数表。对数可以把乘法变成加法，指数变成乘法，因此简化了计算。

举一个计算的例子。假设地球以圆形轨道绕太阳运动，试根据以下已知数据，计算太阳的质量：

• 日地平均距离 \(R = 1.496\times10^{11}\mathrm{\ m}\)
• 地球公转周期 \(T = 3.156\times10^7\mathrm{\ s}\)
• 万有引力常数 \(G = 6.672\times10^{-11}\mathrm{\ m^3/(s^2\cdot kg)}\)

解：根据万有引力定律和牛顿运动定律可知 \[M = \frac{4\pi^2R^3}{GT^2}.\]

这时候如果有电子计算器，只需输入上述数据，就可以直接得到结果。使用对数表需要做如下计算：

\begin{array}{rrr} & \lg G = & \overline{11}.8242 \\ & \lg T = & 7.4991 \\ + & & 7.4991 \\ \hline & \lg GT^2 = & 4.8224 \\[.5em] & \lg R = & 11.1750 \\ \times & & 3\phantom{0} \\ \hline & & 33.5250 \\ & \lg 2\pi = & 0.7982 \\ + & & 0.7982 \\ \hline & \lg 4\pi^2R^3 = & 35.1214 \\ - & \lg GT^2 = & 4.8224 \\ \hline & \lg M = &30.2990 \rlap{\quad = \lg\big(1.991\times10^{30}\big)} \end{array}

计算所得结果为：太阳质量是\(1.991\times10^{30}\mathrm{\ kg}\)。查有关资料可知，准确值为\((1.98855\pm0.00025)\times10^{30}\mathrm{\ kg}\)。¹上述计算的相对误差为0.1%。

电子计算器的普及使我们无需再查阅任何初等函数的表格，不过对于一些非初等函数，仍然常用查表的方法。

前几天有人问我\(\int_0^{\pi/2} \cos^\frac{5}{2} t \mathrm{;d}t\)。我不会，后来查了数学手册，发现了积分公式 \[\int_0^{\pi/2} \sin^{2a+1}t,\cos^{2b+1}t \mathrm{;d}t = \frac{1}{2}B(a+1,b+1) = \frac{\Gamma(a+1)\Gamma(b+1)}{2\Gamma(a+b+2)}.\]

代入\(a=-\frac{1}{2}\), \(b=\frac{5}{4}\)得 \[\int_0^{\pi/2} \cos^\frac{5}{2}t \mathrm{;d}t = \frac{1}{2}B\left(\frac{1}{2},\frac{7}{4}\right) = \frac{\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{7}{4}\right)}{2\Gamma\left(\frac{9}{4}\right)}.\] 根据伽马函数的性质，有\(\Gamma\left(\frac{1}{2}\right)=\sqrt\pi\), \(\Gamma\left(\frac{9}{4}\right)=\frac{\sqrt\pi}{2^{5 / 2}}\frac{\Gamma\left(\frac{7}{2}\right)}{\Gamma\left(\frac{7}{4}\right)}=\frac{15\pi}{32\sqrt2,\Gamma\left(\frac{7}{4}\right)}\), 所以 \[\int_0^{\pi/2} \cos^\frac{5}{2}t \mathrm{;d}t = \frac{16\sqrt2}{15\sqrt\pi}\Gamma^2\left(\frac{7}{4}\right).\]

一般的科学计算器计算器没有计算伽马函数的功能，所以仍然需要使用查表的办法。根据数学手册，\(\Gamma(1.75)=0.91906\)，将此数值代入上式，得 \[\int_0^{\pi/2} \cos^\frac{5}{2}t \mathrm{;d}t = 0.7189.\]

前面用了很多步骤计算一个定积分的值。令人沮丧的是，现在的计算机代数系统甚至可以瞬间给出上述值：WolframAlpha的计算结果。

计算机计算伽马函数，有可能是利用一些近似公式现场计算，也可能是把函数值事先计算好，存在计算机中，然后调出。后面一种情况本质上也是查表，也就是空间换时间。只不过对计算机来说时间太充裕了，像开方、三角函数这样的初等函数，现场计算也用不了多少时间。相比之下，人的计算速度太差，连乘法都要借助表格来节省时间。随着计算机在数值计算领域的发展，所有人工查表的方法恐怕都要渐渐淡出人们的视野了。在它完全消失之前，我还想体验一把。

在一本40年代的《三角学》书中，附录里给出了一份四位对数表，以及详尽的介绍，包括如何从头开始制表。可想而知，那是一份相当艰难的工作。现在，要制一份数学用表无比简单：只需用计算机上的电子试算表软件，输入自变量的值，然后用软件自带的函数功能计算函数值。

我用这种办法制作了一套数学用表，包括：数学常数表、常用对数表、正余{弦,切}×{函数,对数}表、平方数表。这些表格实际上是几十年前的中学生经常用的²。精度取了四位，可以满足我的课堂作业的计算需求；每张表占用2页A4的幅面，非常简洁。

其中，常用对数表用于处理算式中的乘、除、幂和开方。我很少遇到计算中需要取指数和对数的情况，如果有的话，用常用对数表也可以进行计算。所以这张表的价值最高。

4张三角函数的表用来求三角函数，我制表的时候精确到了5分(即0.083°)。实在想要更高精度的话，可以做一点插值，不过计算量就大了。三角函数的对数表很有用，因为实践中三角函数往往和其他数字相乘，直接求得对数，可以节省一次查表的时间。例如计算交流电机的分布系数时，有 \[k_{d\nu} = \frac{\sin\nu\frac{q\alpha}{2}}{q\sin\nu\frac{\alpha}{2}}.\] 化成对数形式 \[\lg k_{d\nu} = \lg\sin\nu\frac{q\alpha}{2} - \lg q - \lg\sin\nu\frac{\alpha}{2}.\] 计算就很方便，因为正弦对数可以通过查表直接得到。

平方数表是后来加上去的。本来用对数表就足够进行平方和开方运算。不过实践发现这样还不够方便。因为勾股定理\(A^2+B^2=C^2\)在计算中经常用到，求其中一个量时需要先计算两个数的平方，然后求和（差），然后再开方。如果用对数表，那么为了求平方需要转换成对数，平方以后为了求和（差）又要转换回真数，来回转换比较繁琐。有了平方表，则可以减少一半的查表步骤，而且简化了计算。

当然还有倒数表、立方数表之类的，这些运算我觉得不如平方来的常见，遇到的时候再用对数表处理应该就够了；所以就没有做。

下面举一个经典的几何问题。如图所示，C, D两地之间因有障碍无法直接测量距离，现在通过A, B两地间接测量，得到4点间的一些距离（已在图中标出）。试求CD。

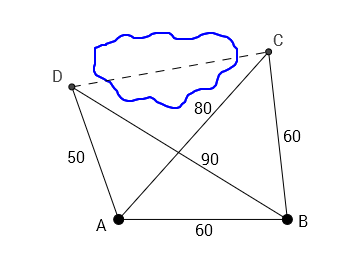
解：求解这个问题需要用到三角学的知识。这里主要用到的是余弦定理 \[a^2 = b^2 + c^2 - 2bc\cos A.\]

在△ACD中，只要求出∠CAD就可以解出CD。而∠CAD=∠BAD-∠BAC。等式右边的两个角分别可以在△BAD和△BAC中解出。按照这个思路计算如下：

\begin{align} \cos\angle BAC &= \frac{80^2 + 60^2 - 60^2}{2\times80\times60} = \phantom{-}\frac{2}{3}, \\\ \cos\angle BAD &= \frac{50^2 + 60^2 - 90^2}{2\times50\times60} = -\frac{1}{3}. \\\ \end{align}

这里碰巧了，给出的边长凑成了整数，所以计算比较简单，笔算即可。如果边长是一般的数值，那么可以借助平方数表快速进行平方的加减运算，然后用对数表计算乘除。计算出余弦的对数值之后，可以不必转换为真数，因为可以直接从正余弦对数表中读出角度值。

下一步有两种做法，一是反向查三角函数表，得出两个角度值，然后做差求出∠CAD。另一种做法是利用三角恒等式，直接求出\(\cos\angle CAD\)。因为这里求出的余弦值比较简单，用后一种做法，计算不会很复杂。

\begin{align} \cos\angle CAD &= \cos(\angle BAD - \angle BAC) \\\ &= \cos\angle BAD \cos\angle BAC + \sin\angle BAD \sin\angle BAC \\\ &= -\frac{1}{3}\times\frac{2}{3} + \sqrt{1-\left(-\frac13\right)^2}\sqrt{1-\left(\frac23\right)^2} \\\ &= \frac{-2+2\sqrt{10}}{9}. \end{align}

因此 \begin{align} CD^2 &= AC^2 + AD^2 - 2AC\cdot AD\cos\angle CAD \\\ &= 80^2 + 50^2 - 2\times80\times50\times\frac{-2+2\sqrt{10}}{9} \\\ &= 8900 - 16000 \times \frac{\sqrt{10}-1}{9}, \end{align} 这时候可以查平方数表，得\(\sqrt{10}=3.162\)，剩下的经过笔算即可得到 \[CD^2=5057.\] 再查平方数表，得\(CD=71\)。

做完这个例子我才发现对数表和三角函数表都没用上。主要是因为给出的数据比较特殊。对于一般的数据，采用查三角函数表然后求角度差来计算∠CAD会比较方便。而在余弦定理的计算中，涉及到乘除的时候，一般还是需要借助对数表。

计算机的历史并不长，但它带来的变革确实异常深刻的。必须承认，常用对数表这样的工具，和计算尺一样已经进入了历史的垃圾堆。更强的计算能力，极大地推动了人类的进步。另一方面，在计算能力低下的年代，虽然社会发展和科学进步非常缓慢，但是偶尔还是会取得突破性的进展。那些先辈靠着原始的工具，能发现宇宙的运行规律，造的了火车飞机轮船，取得那样伟大的成就，是非常了不起的。据我所知，开普勒在计算行星轨道数据的时候，对数尚未发明。这样的情境是今人无法想象的吧。