快速二-十进制转换
将计算机内部存储的二进制数值转换为十进制以供输出是一件常见的工作。在一些场合,需要大量进行这种转换,这时希望速度能尽可能地快。
二–十进制转换大量用到整数除法和取余运算。朴素的教科书算法是这样的:
do {
putchar(n % 10);
n /= 10;
} while (n);
当然,输出是逆序的。这并不是什么本质的问题,实际代码再加上逆序的处理就可以了。
这种做法每个循环计算一次取余和一次除法。我现在有一个硬件(Nios II/e),没有硬件乘法器和除法器。乘除运算使用软件模拟,速度非常慢。软件模拟的除法,并不能同时得到商和余数。也就是说,为了得到商和余数,除法会被计算两遍。(这是编译器的优化问题,理论上可以通过改进编译器的优化能力解决)。
实际上,一旦得到了商,不必再做一次除法,就可以得到余数:
do {
unsigned q, r;
q = n / 10;
r = n - q * 10;
putchar(r);
n = q;
} while (n);
对于一般的处理器,一次乘法加上一次减法所用的时间也比一次取余运算来得短。在没有硬件乘法器的情况下,那么最好连乘法也不要用,可以使用移位运算代替。根据这个思想,我就可以写出第一个实用版本:
char *simple(int n)
{
static char buffer[11];
char *p = buffer + 10;
do {
unsigned q, r;
q = n / 10;
r = n - (q << 1) - (q << 3);
*--p = '0' + r;
n = q;
} while (n);
return p;
}
对照组则选择C标准库的itoa函数。当然,itoa还处理了负数的情况,而我假设输入是正数。
char *lib(int n)
{
static char buf[12];
return itoa(n, buf, 10);
}
做一下benchmark,每个函数循环20000次,结果是simple执行了2323个ticks(我的系统上一个tick是1毫秒,50000个时钟周期),而lib执行了5137个ticks。看得出来,标准库的实现是最朴素的算法,而编译器也未能恰当地优化。调查一下反汇编代码,确实如此,分别调用了编译器生成的__umodsi3和__udivsi3(软件模拟的取余和除法)。
Hacker’s Delight
既然标题叫做“快速二–十进制转换”,那么一定要拿出一些dirty hacks才好。有一本书叫做Hacker’s Delight,里面就全是这些东西,当然也提到了整数除法的快速计算。其中包括除以10的算法:
unsigned divu10(unsigned n) {
unsigned q, r;
q = (n >> 1) + (n >> 2);
q = q + (q >> 4);
q = q + (q >> 8);
q = q + (q >> 16);
q = q >> 3;
r = n - q*10;
return q + ((r + 6) >> 4);
// return q + (r > 9);
}
算法原理在书中有说明。这个函数给出商,可以用商计算出余数,或者对这个函数稍加修改,同时得到商和余数。
我把上面这段代码稍加修改(例如把*10改成位运算),替换掉simple中的相应部分,定义了一个新的函数hacker。这个函数只包含机器指令,没有软件模拟的运算(乘、除)。benchmark的结果为392个ticks。比simple快了6倍。
软件优化似乎已经到达了尽头。因为Nios II是软核处理器,当然也可以通过修改硬件来解决问题,例如增加硬件除法器等。不过,对于“除以常数10”这个任务来说,Hacker’s Delight版本的算法通常比硬件除法还要快。
一个了不起的办法是定制专用的“除以10”电路,配合Nios II的自定义指令功能。这只有像Nios II这样的运行在FPGA上的软核系统才能做到。
创建一个除法器,可以使用Altera提供的LPM_DIVIDE模板生成一个31位/4位无符号除法器(我假定输入int为正数,所以被除数31位就够了,而且这样可以保证商+余数总共不超过32位),然后把除数直接连线为常数10。或者把上面Hacker’s Delight的C代码翻译成Verilog(基本上不用改),就构造了一个专用的除以10的除法器。
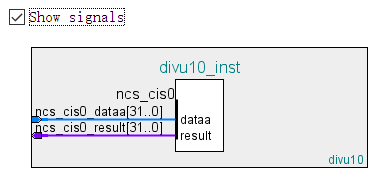
然后创建一个新的模块,用来表示Nios II的一条自定义指令
module divu10_ci
(
input [31:0] ncs_cis0_dataa,
output [31:0] ncs_cis0_result
);
把ncs_cis0_dataa[30:0]连接到除法器的被除数,ncs_cis0_result[31:4]连接到商,ncs_cis0_result[3:0]连接到余数。这样自定义语句的硬件模块就做好了。
接下来要在Qsys中创建自定义语句。在Component Editor中有一个模板Nios Custom Instruction Slave - Combinational,点击之后设置相关属性。最主要的是在Files选项卡中把刚才编写的divu10_ci硬件模块添加进去。
接下来只需要把创建好的Qsys组件加入系统,然后重新生成HDL,重新综合电路。在软件端,需要重新生成BSP。新生成的system.h就会含有为自定义指令定义好的宏
#define ALT_CI_DIVU10(A) __builtin_custom_ini(ALT_CI_DIVU10_N,(A))
#define ALT_CI_DIVU10_N 0x0
这样,求除以10的商和余数可以这样写:
q = ALT_CI_DIVU10(n);
r = q & 0xf;
q >>= 3;
总共只有3条机器指令
2009c032 custom 0,r4,r4,zero
20c003cc andi r3,r4,15
2008d13a srli r4,r4,4
想必运行时间也大大减少了。benchmark的结果为127个ticks,比hacker又快了3倍。
TL;DR
这是各种做法的benchmark结果:
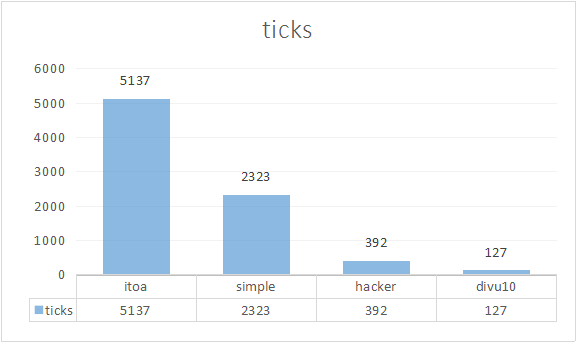
总结:Hacker’s Delight是最通用的,而且相当快。专用电路是最快的,但是必须有可定制的硬件才能实现。同时计算商和余数时,调查一下处理器是否需要计算两次除法,如果是,可以把计算余数改用乘法来做。(如果处理器本来就可以同时计算商和余数,那就没必要这么改了,反而会影响编译器的优化)。标准库是最慢的(另:div能同时计算商和余数,但其实它还是做了和一次/加一次%)。