微分方程的数值解法是一个庞大的话题。这里描述一种简单的、容易想到的数值解法，它可以用简单的计算机程序实现。

以微分方程 \[\frac{dv}{dt} + v = \sin t\] 为例，这是一个一阶线性微分方程。求解的时候，把时间离散化，即\(t=n\Delta T\)，\(\Delta T\)是最小的时间单位。假设我们只关心\(t\geq 0\)时的解，那么\(n\)是自然数。

考虑导数的定义 \[\frac{dv}{dt} = \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \lim_{\Delta t \to 0} \frac{v(t)-v(t-\Delta t)}{\Delta t}.\] 在离散化的时间里，我们不可能让\(\Delta t\)无穷小，最小也只能等于时间单位\(\Delta T\)。所以时间离散化以后，我们用\(\frac{\Delta v}{\Delta T}\)来代替导数\(\frac{dv}{dt}\)。

在一个\(\Delta T\)内，\(v\)的增量\(\Delta v = v(t) - v(t-\Delta T)\)。为了书写方便，我们用记号\(v[n]\)表示\(v(n\Delta T)\)。考虑到\(t=n\Delta T\)，有 \[\Delta v = v[n] - v[n-1].\]

于是，原来的微分方程就可以写成离散的形式 \[\frac{v[n]-v[n-1]}{\Delta T} + v[n] = \sin t.\] 将\(v[n]\)解出，得 \[v[n] = \frac{v[n-1] + \Delta T\sin t}{1+\Delta T}.\] 这就是一个递推式，给定初始值\(v[0]\)，就可以递推地计算出后续的所有\(v[n]\).

例如，给定\(v[0] = 0\)，并且取\(\Delta T = 0.04\)，则计算得如下结果(x*是微分方程的解析解\(v(t)=\frac{1}{2}\left(\sin t - \cos t + \mathrm{e}^{-t}\right)\)在相应时刻的值)：

t       x               x*
0       0               0
0.04    0.001538051     0.000789333
0.08    0.004552538     0.003114667
0.12    0.008981756     0.006912004
0.16    0.014763927     0.012117356
0.2     0.021837212     0.018666753
0.24    0.030139728     0.026496256
0.28    0.039609571     0.035541976
0.32    0.05018484      0.04574009
0.36    0.061803662     0.057026868
0.4     0.074404227     0.069338697

更多数据已经省略。将这些数值制成图表，如下所示：

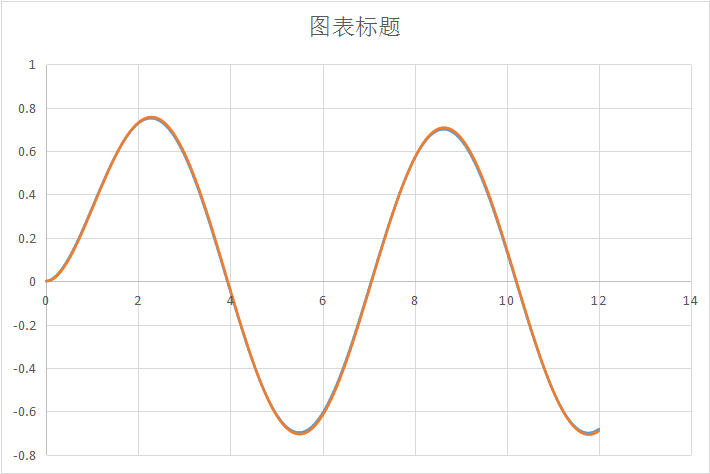
蓝色的曲线是数值解，橙色的曲线是解析解。从图形可以看出，两者的重合度很高。一般来说，\(\Delta T\)取得越小，时间划分得越细腻，数值解也就越精确。

对于高阶的线性微分方程，可以通过一种巧妙的办法转化成一阶微分方程，然后求解。以 \[\ddot{x} + x = \sin t\] 为例，这是一个二阶线性微分方程。把\(x\)和\(x\)的一阶导数\(\dot{x}\)分别设成两个变量 \[ \begin{aligned} x_1 &= x, \\ x_2 &= \dot{x}. \end{aligned} \] 则 \[ \begin{aligned} \dot{x}_1 &= x_2, \\ \dot{x}_2 &= \sin t - x_1. \end{aligned} \] 或者写成矩阵形式 \[\boldsymbol{\dot{x}} = \boldsymbol{Ax} + \boldsymbol{B}u,\] 其中\(\boldsymbol{A}=\left[\begin{smallmatrix}0&1 \\ -1&0\end{smallmatrix}\right]\)，\(\boldsymbol{B}=\left[\begin{smallmatrix}0 \\ 1\end{smallmatrix}\right]\)，\(\boldsymbol{x} = \left[\begin{smallmatrix}x_1 \\ x_2\end{smallmatrix}\right]\)，\(u = \sin t\)。这就是一个一阶微分方程的形式了（尽管变量是多维的向量）。

根据时间离散化的原则，将微分方程写成离散形式 \[\frac{\boldsymbol{x}[n]-\boldsymbol{x}[n-1]}{\Delta T} = \boldsymbol{Ax}[n] + \boldsymbol{B}u.\] 解出 \[\boldsymbol{x}[n] = (\boldsymbol{I}-\boldsymbol{A}\Delta T)^{-1}(\boldsymbol{x}[n-1]+\boldsymbol{B}u\Delta T).\]

对于本例而言，将\(\boldsymbol{A}=\left[\begin{smallmatrix}0&1 \\ -1&0\end{smallmatrix}\right]\)代入，并取\(\Delta T = 0.04\)，得 \[(\boldsymbol{I}-\boldsymbol{A}\Delta T)^{-1} = \frac{1}{\Delta T^2 + 1}\begin{bmatrix}1&\Delta T\\-\Delta T&1\end{bmatrix} = \frac{1}{626}\begin{bmatrix}625&25\\-25&625\end{bmatrix}.\]

也可以再把矩阵形式的递推式写成标量形式 \[ \begin{aligned} x_1[n] &= \frac{625}{626}x_1[n-1] + \frac{25}{626}(x_2[n-1] + \Delta T\sin t), \\ x_2[n] &= -\frac{25}{626}x_1[n-1] + \frac{625}{626}(x_2[n-1] + \Delta T\sin t). \end{aligned} \]

给定\(\boldsymbol{x}[0] = \left[\begin{smallmatrix} 0\\0 \end{smallmatrix}\right]\)，根据递推式计算的结果如下(x*为微分方程的解析解\(x(t) = \frac{1}{2}(\sin t - t\cos t)\)在相应时刻的值)：

t       x1              x2              x*
0       0               0               0
0.04    6.38807E-05     0.001597018     1.0665E-05
0.08    0.000255217     0.004783397     8.52787E-05
0.12    0.000637073     0.009546403     0.000287585
0.16    0.001271803     0.015868259     0.000680921
0.2     0.002220851     0.023726198     0.001328008
0.24    0.003544552     0.033092521     0.002290756
0.28    0.005301939     0.043934669     0.003630063
0.32    0.007550551     0.05621531      0.005405613
0.36    0.010346248     0.069892429     0.007675688
0.4     0.013743026     0.084919442     0.010496972

计算出来的\(x_1\)就是我们所需的\(x(t)\)在离散时刻的值。我们顺便还把各时刻\(x\)的导数\(\dot{x}(t)\)也计算了出来，也就是\(x_2\)。虽然可能并不需要这些数据，但是它们在求解过程中有用。

将x1和x*制成图表，如下所示：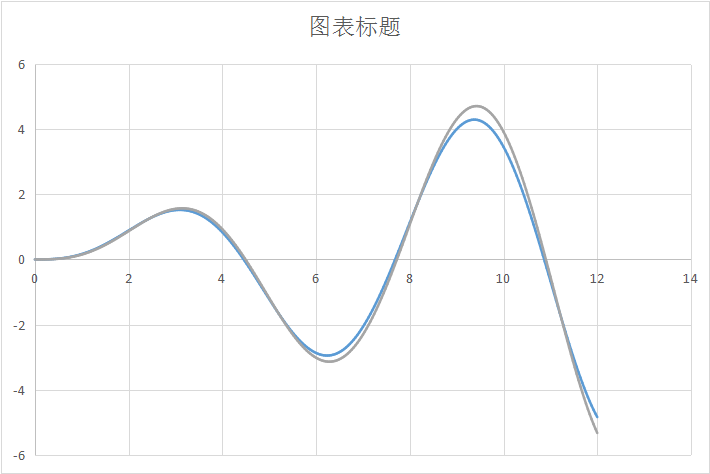

蓝色的曲线是数值解，灰色的曲线是解析解。可见，数值方法所求出来的解基本上拟合了解析解。但是，误差也是逐渐扩大的。