前天下午打牌，触景生情想起了一个概率论的问题：3个人打一副扑克（A23456789 10 JQK各4张+大小王=54张牌），随机发牌，每人拿18张。设随机变量X表示三个手中的炸弹（指4张点数相同的牌）的总数，求X的分布律。

这样的问题理论上应该可以使用古典概型来求解。但是我想了一会之后就放弃了。为了对这个问题有一个大概的了解，我写了一段程序模拟洗牌和发牌的过程并且统计其中的炸弹个数。

从程序的输出中我得到了一个有趣的结果。下面是某一百万次试验中得到的统计结果：

685121
259261
49135
5935
520
28
0

从上到下依次是X=0,1,2……的频数。6个炸弹以上的情况没有出现。

下面是条形统计图，可见，随着炸弹数增加，频数迅速减小。概率最大的事件是没有炸弹。炸弹个数不超过1个的频率高达94%，这和我平时打牌的常识相符合。

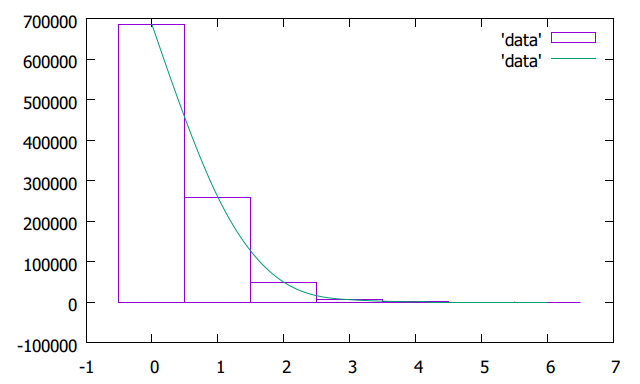
对此数据稍加分析，就会得到有趣的结果。这学期我学了《概率论与数理统计》这门课程。对于离散型的随机变量，讲过好几种典型的分布。对于图中这种迅速下降的情况，看上去有点像泊松分布。那么，有没有可能是泊松分布呢？

假设X服从泊松分布，那么分布律是\(P\{X=k\}={\lambda^k{\rm e}^{-\lambda}\over k!}\)。可以使用最大似然估计法估计其中参数\(\lambda\)的值。做法如下：

根据已给出的样本，做出似然函数 \[L(\lambda) = \prod_{k=0}^\infty (P\{X=k\})^{f_k}\] 其中，\(f_k\)是事件\(X=k\)的频数。注意，形式上有无穷个因子，但实际上因为\(f_k\)只有有限项不为0，实际上只是有限个因子的乘积。

取对数 \[ \ln L(\lambda) = \sum_{k=0}^\infty f_k \ln P\{X=k\} = \sum_{k=0}^\infty f_k (k\ln\lambda - \lambda - \ln{k!})\]

求导 \[ {{\rm d} \over {\rm d}\lambda} \ln{L(\lambda)} = \sum_{k=0}^\infty f_k \left({k\over\lambda} - 1\right) \]

令导数等于0，可以解得参数的估计值 \[ \hat\lambda = {\sum_{k=0}^\infty k f_k \over \sum_{k=0}^\infty f_k} \]

到此，我发现泊松分布的参数估计是一个非常简单的表达式，即炸弹个数的加权平均数。这个估计是有道理的，因为在泊松分布中，\(\lambda\)的意义是总体的期望值。用样本(的平均值)估计总体(的期望值)，就是统计学的原理。

代入数值得 \[\hat\lambda = {0\cdot685121 + 1\cdot259261 + 2\cdot49135 + 3\cdot5935 + 4\cdot520 + 5\cdot28 \over 1000000} = 0.377556\]

将这个估计参数代入泊松分布的表达式，得到的分布律和统计数据非常吻合（特别是X较小的情况）。因为我没有学过分布拟合检验，所以现在没法检验这个分布的拟合程度。我用Excel随便算了一下，以供参考：