TL;DR
将计算机内部存储的二进制数值转换为十进制以供输出是一件常见的工作。在一些场合,需要大量进行这种转换,这时希望速度能尽可能地快。
二–十进制转换大量用到整数除法和取余运算。朴素的教科书算法是这样的:
do {
putchar(n % 10);
n /= 10;
} while (n);
当然,输出是逆序的。这并不是什么本质的问题,实际代码再加上逆序的处理就可以了。
这种做法每个循环计算一次取余和一次除法。我现在有一个硬件(Nios II/e),没有硬件乘法器和除法器。乘除运算使用软件模拟,速度非常慢。软件模拟的除法,并不能同时得到商和余数。也就是说,为了得到商和余数,除法会被计算两遍。(这是编译器的优化问题,理论上可以通过改进编译器的优化能力解决)。
继续阅读 →TL;DR
数码管一般用来显示的数字,通常由7个笔画构成(有的还有1个小数点),所以也称为7段数码管。之前构建的Nios II系统就用了6个数码管输出信息。
传统上,要使用数码管,需要译码器将二进制编码的数字转换成7个笔画的编码,例如TTL的7447和CMOS的4511集成电路。
给每个数码管配置一个译码器,并且将每一位数字同时传送到各译码器上,这种方案叫做静态显示。静态显示原理简单,但是浪费硬件资源。
将译码器分时复用则构成动态显示电路:在一个时刻只点亮一个数码管,并使用一个扫描电路轮流扫描各个数码管。当扫描频率足够高时,显示的效果就像是所有数码管同时都被点亮。
继续阅读 →我用Go编写了一个简单的聊天室程序。这个程序分为服务器端和客户端两部分。
服务器端用于监听主机上的端口,以便接受来自其他主机的连接。建立连接后,服务器从客户端处收集消息,然后广播到所有客户端。
客户端用于消息的输入和显示。当成功建立起到主机的连接后,输入的消息将被发送至服务器,而服务器发来的消息将被显示在屏幕上。
我用termui编写客户端的界面。虽然还有一些小问题,总体来说效果不错。
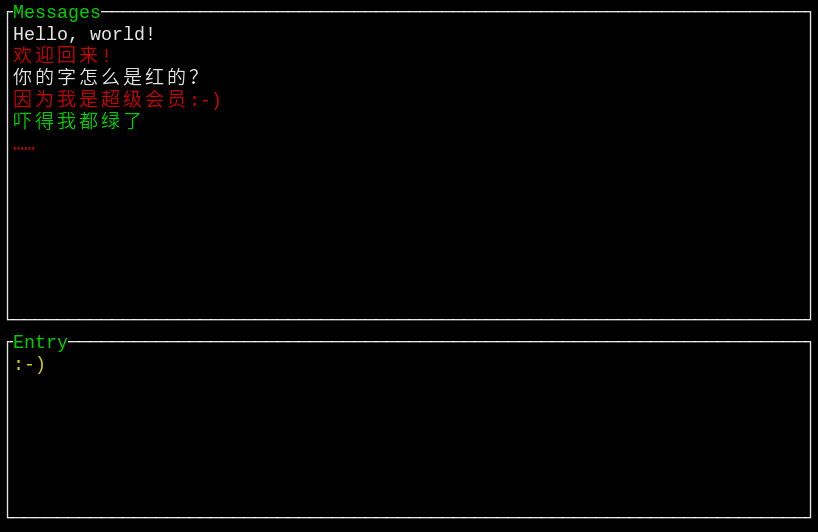 继续阅读 →
继续阅读 →GNU Privacy Guard简称GnuPG或GPG,是一款密码学工具。许多Linux系统上自带的gpg命令就是它。其最重要的功能是对数据进行加密、解密和签名。此外还带有密钥生成和管理功能。
GPG区别于一般加密工具的地方在于其使用非对称加密机制。加密时,使用收件人的公开密钥,该密钥公开发行可供所有人使用。解密时,使用收件人的私有密钥,该密钥由收件人严密保管。这样,收件人无需和发件人商定密码,就可以安全地通信。
签名是确保信息完整性的办法。使用发件人的私有密钥进行签名,其他人无法伪造,但所有人均可使用发件人的公开密钥进行验证。
我用GPG生成了一个密钥对,公共密钥已经上传到密钥服务器上,大家可以通过
gpg --recv-keys 0DB87340
下载这个密钥。其指纹为
2252 7AF4 8AFB 5635 72EC AC4D 895C 7F46 0DB8 7340
理论上,如果有人要冒充我的身份,只需创造一个虚假的密钥上传到服务器,然后入侵存放这个页面的服务器,纂改上面的密钥编号和指纹。
当然要这么做也有一定难度,总之小心为好,导入密钥的时候务必需要通过可靠的方式(例如,当面)和密钥的持有人进行确认,然后对它签名,以示信任。
继续阅读 →相差八度的两个音,在频率上相差了一倍。例如,A4的频率为440Hz,而A5的频率为880Hz,A3的频率则为220Hz。人耳听起来“距离相等”的若干个音,频率并非成等差数列,而是成等比数列。
“八度”的称谓源于八个频率递增的音,例如
C4 D4 E4 F4 G4 A4 B4 C5
它们构成C大调音阶,唱作do re mi fa so la si do(高)。有意思的是,音阶中的各个音也不是“等距离”分布的。音乐老师说过,mi和fa、si和do之间只相差半音,而其他相邻的音之间相差全音。
相差全音的两个音之间,还存在一个音,和这两个音的距离都是“半音”。例如,C4和D4之间的音,可以记作C♯4或者D♭4。如果把这些音也插进音阶里,就变成了13个音:
C4 C♯4 D4 D♯4 E4 F4 F♯4 G4 G♯4 A4 A♯4 B4 C5
这样一来,相邻的音的“距离”都相等。也就是说,这些音的频率成等比数列。相隔12个间隔的两个音的频率为2倍关系,即\(q^{12}=2\),\(q\)为公比,或者说是相邻两个音的频率之比。由此得\(q = \sqrt[12]{2}\approx 1.059463\)。这个规律最早由明朝的朱载堉提出,现在称为十二平均律。
知道了十二平均律,再根据一个基准音的频率(如A4为440Hz),就可以推算出所有音的频率。
继续阅读 →多重继承是面向对象编程(Object Oriented Programming, OOP)中的一个有争议的话题。并非所有OOP语言都支持多重继承(Java和C#均不支持)。C++作为万能语言是支持多重继承的典型例子,即便如此,一些C++的开发框架,例如MFC,也从不使用多重继承特性。Go虽然很少用到复杂的继承,但是它本身是支持多重继承的。
我想从对象的存储方式角度来分析多重继承和虚基类的问题。C++在这方面有些故弄玄虚,一个virtual关键字弄得让人有些摸不着头脑。Go的设计在提供多重继承功能的同时,也非常明确地指出了对象在内存中的存储形式,理解起来也容易许多。
继续阅读 →幻方(magic square)是休闲数学(recreational mathematics)所感兴趣的话题。相传在古代曾有神龟浮出水面,背上有图案,称为《洛书》:
载九履一,左三右七,二四为肩,六八为足,五居中腹。
这是一个3阶幻方,如下所示。它的特点是每行、每列、每条对角线上的数字之和都相等。
4 9 2
3 5 7
8 1 6
继续阅读 →我以前用C写过一个简单的解释器,它接受类似BASIC的代码,并解释执行。一个解释器主要包含以下部分:
- 词法分析器(lexer),用来把代码分割成一连串记号(token),如标识符、数字、运算符等,并且忽略空白和注释。
- 语法分析器(parser),用来分析代码的层次结构,并构造抽象语法树(AST)。
- 后端(backend),用来解释执行所生成的AST。
如果是编译器,那么后端的作用是生成机器代码,以便直接被CPU执行。
词法分析器可以手写也可以用lex自动生成。因为比较简单,所以往往采用手写的方式。语法分析器可以手写,通常采用递归下降(recursive-descent)算法;也可以用yacc自动生成,后者使用的是一种称为LALR(1)的技术。
最近发现Go的官方工具链自带了一个yacc工具(go tool yacc),所以就试着用它写了一个类似的解释器。功能被进一步削减,只能算是一个demo。
能解释运行像这样的代码:
SUM = 0
I = 1
WHILE NOT I > 100 DO
SUM = SUM + I
I = I + 1
END WHILE
PRINT SUM
继续阅读 →Go从1.5版本开始支持动态链接库。目前官方工具链仅在linux-amd64平台支持动态链接;gccgo则支持更多的平台。
在此之前,Go的所有程序都采用静态链接。一个很简单的"hello, world"程序,因为引入了fmt库(这个库进一步依赖其他代码),所以最终得到的可执行文件也比较大。如果将Go的标准库编译为动态链接库,就可以减小Go生成的可执行文件的大小。
我在Gentoo上安装了Go 1.6.3,要将标准库编译为动态链接库,需要以root权限执行
go build -buildmode=shared -linkshared std
这样就会产生/usr/lib/go/pkg/linux_amd64/dynlink/libstd.so文件。这个文件在我的机器上有32MB大,包含了Go标准库的所有内容。
继续阅读 →生成器(generator)是Python的一个语法特性,例如生成平方数序列的生成器可以写成
def squares(n):
i = 1
while i <= n:
yield i * i
i += 1
若要求前10个平方数之和,只需
>>> sum(squares(10))
385
在Go语言中,使用goroutine配合channel,可以实现相同的功能:
func squares(n int) <-chan int {
ch := make(chan int)
go func() {
for i := 1; i <= n; i++ {
ch <- i * i
}
close(ch)
}()
return ch
}
然后可以用for语句遍历:
sum := 0
for term := range squares(10) {
sum += term
}
继续阅读 →