我一直用一个简单的近似公式来估算一个数的平方根： \[\sqrt{n^2+d} \approx n + \frac{d}{2n}.\]

例如我想估算10的算术平方根，心中默想\(10=3^2+1\)，于是\(\sqrt{10}\approx 3+\frac{1}{6} = 3.167\)。这个方法非常简单有效。

我不知道以前的算术课程是否要讲授笔算开方的方法。反正自从电子计算器普及，这些技术就无人问津了。有一种竖式方法可以用来做任意位数的开方运算，如下图所示：

Golang Project页面右侧有一张图片：

一只gopher拿着游标卡尺，工程师的经典工具。另一只gopher拿的东西现在很少见了，叫做计算尺(slide rule)。它曾经也是科学技术人员必备的工具，可以不打草稿进行乘除运算，常见的有3位有效数字，能满足一般的工程需要。

自从1972年手持式科学计算器HP-35面市，计算尺迅速被淘汰。科学计算器运算速度快、精度高、功能丰富，各方面指标完胜已有的计算工具。现在已经没有厂家生产计算尺；它已成为一种收藏品。

另一个同样被淘汰的工具是算盘。这个工具在中国非常流行。有意思的是，算盘是数字式的，它本身只能处理离散值，不存在失真的问题，精度高。相比之下计算尺是模拟式的，理论上有无限的精度，但是因为存在加工精度限制、装配误差等，实际上精度并不高。电子计算器普及后，算盘也被淘汰了。耐人寻味的是，现在仍然有厂家生产算盘。

这里还要提一个因科学计算器普及而变得过时的技术：常用对数表。对数可以把乘法变成加法，指数变成乘法，因此简化了计算。

货币的时间价值是利息的(理论)来源。利息的计算是一个很有意思的问题。单利和复利属于比较简单的计算。 设一笔资金的现值是\(\text{PV}\)，每期利率是\(r\)，那么\(N\)期之后，按照复利计算，它的价值\[\text{FV} = \text{PV}\left(1+r\right)^N.\] 这就是著名的复利公式。

当每期都有新投入的现金时，就变得复杂起来。举个例子：银行贷款提供两种分期还款的方式：等额本息和等额本金。怎样计算每期应当偿还的金额？

等额本息

等额本息，即在每期末偿还一笔相同的金额\(\text{PMT}\)（也有在每期初还款的，暂不讨论这种情况），其中一部分是上期余额产生的利息，剩下的是偿还的本金。上期余额扣除本期偿还的本金后，成为本期余额……这个过程看起来挺复杂，其实利用货币的时间价值很容易算出\(\text{PMT}\)：把每期支付的金额归算为现值：

• 第1期：\(\frac{\text{PMT}}{1+r}\)
• 第2期：\(\frac{\text{PMT}}{(1+r)^2}\)
• …
• 第N期：\(\frac{\text{PMT}}{(1+r)^N}\)

将它们相加，总的现值 \begin{align} \text{PV} &= \text{PMT}\left[(1+r)^{-1} + (1+r)^{-2} + \cdots + (1+r)^{-N} \right] \\\ &= \text{PMT} \frac{(1+r)^{-1}\left[1-(1+r)^{-N}\right]}{1-(1+r)^{-1}} \\\ &= \text{PMT} \frac{1-(1+r)^{-N}}{r}. \end{align} 这也就是你每期支付\(\text{PMT}\)的情况下，银行愿意贷款给你的金额。反过来说，如果你打算贷款\(x\)，就可以根据此式算出每期的还款额 \[\text{PMT} = \frac{r}{1-(1+r)^{-N}} x.\]

为了提高功率因数，在变压器二次侧进行无功补偿。现在需要使得一次侧的功率因数不低于0.9，那么二次侧的功率因数肯定需要补偿到0.9以上，补偿到多少合适呢？

一个经验值是，二次侧功率因数补偿到0.92，可以使一次侧功率因数约等于0.9。这个数值是怎么得到的呢？

设二次侧的视在功率是\(S_2\)，功率因数角是\(\varphi_2\)。则二次侧的有功功率 \[P_2=S_2\cos\varphi_2,\] 无功功率 \[Q_2=S_2\sin\varphi_2.\]

变压器会带来额外的损耗，而且以无功居多，这也是导致一次侧功率因数低于二次侧的原因。为了定量地分析，需要一些额外的参数。典型的变压器消耗的有功功率 \[\Delta P_T\approx 0.015S_2,\] 无功功率 \[\Delta Q_T\approx 0.06S_2.\] 由此可知一次侧的有功功率 \[P_1=P_2+\Delta P_T=S_2(\cos\varphi_2 + 0.015),\tag{1}\] 无功功率 \[Q_1=Q_2+\Delta Q_T=S_2(\sin\varphi_2 + 0.06).\tag{2}\]

PIC是Microchip公司生产的微控制器，有8位、16位、32位的型号。其中PIC12系列为8引脚8位微控制器，它的引脚数非常少，很适合做一些小型项目。例如最简单的流水灯，如果用微控制器来做，那么就不需要其他IC芯片了（振荡器为微控制器自带，而移位寄存器的功能可以用软件实现）。

我有一片PIC12F629和一片PIC12F675。两者功能基本一致，后者多了A/D功能。之前我尝试自制PIC编程器给629编程，试了很久也没有成功，只好买了一个正规的编程器来用，结果发现629似乎被我折腾坏了。现在只剩下一片675，我用它制作了两个小项目：音乐播放器和字符显示器。

流水灯是一种非常简单的电路设计项目。使用移位寄存器很容易实现这个电路：

制作需要打印的文件的时候，插图的分辨率一定要足够高，否则看起来的效果十分恶心：

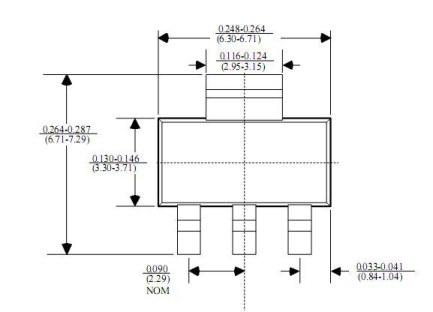
像这种在屏幕上显示就已经糊了的图（可能是在放大比例不正确的情况下通过截图得到的），打印出来更是惨不忍睹。

文档中许多非照片类的插图，如示意图、流程图等，可以用PSTricks来画，画出来的是高质量的矢量图，这样就无需关心分辨率的问题。

下图是我用PSTricks画的同一个零件的图纸。实际上，对于零件图纸，我觉得最好的方案是直接用CAD软件导出矢量图(SVG或者PostScript)，非常省事。(但是似乎不是所有CAD软件都有导出矢量图的选项。)

TL;DR

将计算机内部存储的二进制数值转换为十进制以供输出是一件常见的工作。在一些场合，需要大量进行这种转换，这时希望速度能尽可能地快。

二–十进制转换大量用到整数除法和取余运算。朴素的教科书算法是这样的：

do {
	putchar(n % 10);
	n /= 10;
} while (n);

当然，输出是逆序的。这并不是什么本质的问题，实际代码再加上逆序的处理就可以了。

这种做法每个循环计算一次取余和一次除法。我现在有一个硬件（Nios II/e），没有硬件乘法器和除法器。乘除运算使用软件模拟，速度非常慢。软件模拟的除法，并不能同时得到商和余数。也就是说，为了得到商和余数，除法会被计算两遍。（这是编译器的优化问题，理论上可以通过改进编译器的优化能力解决）。

TL;DR

数码管一般用来显示的数字，通常由7个笔画构成(有的还有1个小数点)，所以也称为7段数码管。之前构建的Nios II系统就用了6个数码管输出信息。

传统上，要使用数码管，需要译码器将二进制编码的数字转换成7个笔画的编码，例如TTL的7447和CMOS的4511集成电路。

给每个数码管配置一个译码器，并且将每一位数字同时传送到各译码器上，这种方案叫做静态显示。静态显示原理简单，但是浪费硬件资源。

将译码器分时复用则构成动态显示电路：在一个时刻只点亮一个数码管，并使用一个扫描电路轮流扫描各个数码管。当扫描频率足够高时，显示的效果就像是所有数码管同时都被点亮。

我用Go编写了一个简单的聊天室程序。这个程序分为服务器端和客户端两部分。

服务器端用于监听主机上的端口，以便接受来自其他主机的连接。建立连接后，服务器从客户端处收集消息，然后广播到所有客户端。

客户端用于消息的输入和显示。当成功建立起到主机的连接后，输入的消息将被发送至服务器，而服务器发来的消息将被显示在屏幕上。

我用termui编写客户端的界面。虽然还有一些小问题，总体来说效果不错。