2018-6-9 更新： 文中部分过时信息已用删除线划去。

之前几天重新配置了我的 Gentoo 桌面环境。很遗憾的是官方源中的 Gnome 在不用 systemd 的情况下是无法顺利安装的，我暂时不打算更换整个 init 系统，所以我先装了 Xfce 凑合。（除了功能稍显单薄，Xfce 的各方面我都很喜欢，可能是因为它是我用过的第一个 Linux 桌面环境。）

rui@localhost ~ $ uname -a
Linux localhost 4.14.8-gentoo-r1 #6 SMP Mon Dec 25 16:54:41 EST 2017 x86_64 Intel(R) Core(TM) i7-6500U CPU @ 2.50GHz GenuineIntel GNU/Linux

IBus (Intelligent Input Bus) 是 Unix 系统上可用的一种输入法框架。我尝试自制了一个简单的“查表”式的输入法，类似于用微软的IME编辑器生成的古老输入法。

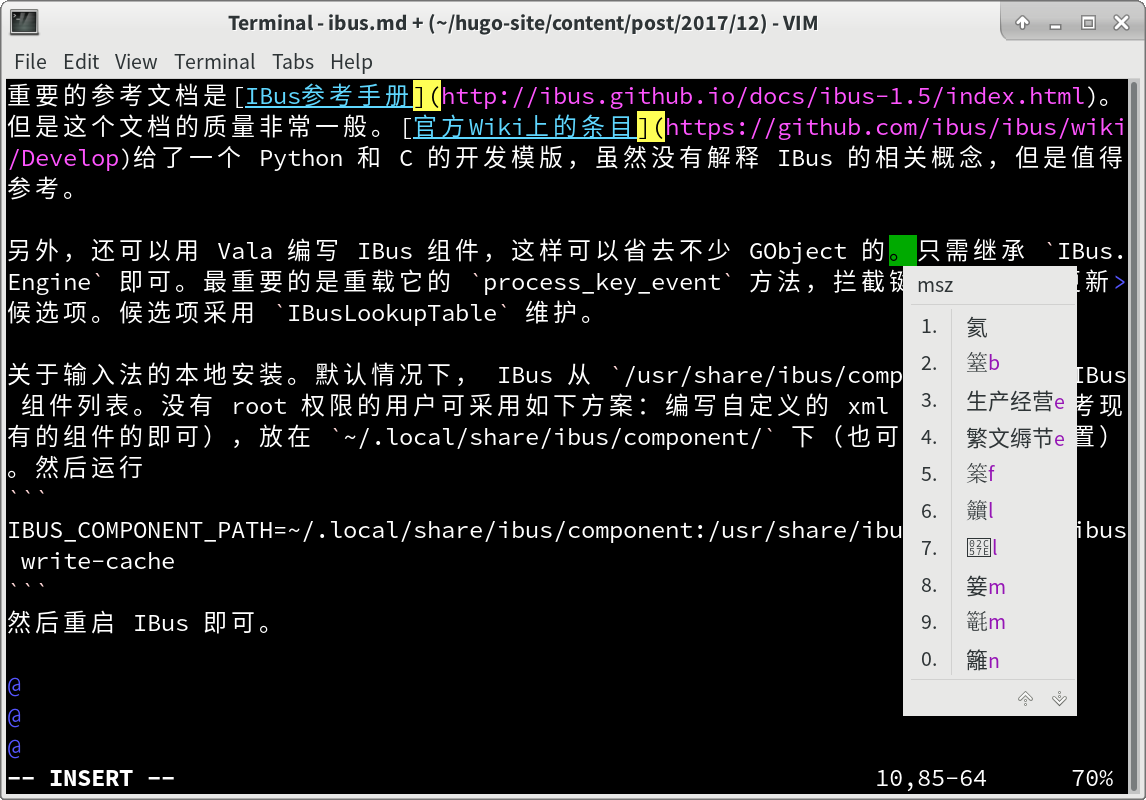
重要的参考文档是IBus参考手册。但是这个文档的质量非常一般。官方Wiki上的条目给了一个 Python 和 C 的开发模版，虽然没有解释 IBus 的相关概念，但是值得参考。

另外，还可以用 Vala 编写 IBus 组件，这样可以省去不少 GObject 的繁文缛节。只需继承 IBus.Engine 即可。最重要的是重载它的 process_key_event 方法，拦截键盘输入，并更新候选项。候选项采用 IBusLookupTable 维护。

画图是观察数据结构的好办法。 二叉树是一种常见的数据结构， 我在调试的时候往往通过先序遍历把整个树的结构打印出来。 然后拿一张草稿纸， 根据打印出的信息， 用笔画出整个树的样子， 然后判断该进行什么操作 （或者我已经执行的操作是否正确）。

为了偷懒， 我在想有没有办法能够让计算机自动生成二叉树的图像。 我发现使用 MetaPost 可以方便地实现。

MetaPost是非常经典的矢量图绘制工具。¹ 之前我用 PSTricks 配合 XeTeX 绘制含中文标签的图形，因为 MetaPost 中不方便使用中文标签。确实如此。

TL; DR 目前比较简单的办法是用 LuaTeX，因为它内置了 MetaPost 库 MPLib，可以直接输出 PDF，字体部分由 LuaTeX 负责处理。

(La)TeX 常被视为高质量出版工具。 确实如此， 但并非用它们生成的文档必然具备较高的排版质量： 计算机工具始终遵守人的指令， 因此排版质量的最终决定者仍然是作者本身。

LaTeX 给人一种快速上手的感觉， 某些作者可能愿意简单地将自己的文档按照结构化的方式以 LaTeX 代码呈现， 剩下的排版细节留给宏包以及排版引擎。 （某种程度上讲这也是 LaTeX 的设计目标之一。）

Plain TeX 相对而言要求作者对排版细节知悉更多。 例如， 它要求用户手动添加 {\it 斜体修正\/} 。 这看起来毫无必要， 并且丝毫不 “智能”； LaTeX 的 \textit{斜体} 功能就自动在末尾添加了斜体修正。

下面考虑一个 TeX 中比较麻烦的问题： 表格排版。 理论上， 可以把表格内的数据分离出来， 只需套用所需的格式， 就可以排版表格。 但是实践中往往需要手动地调整表格的样式。 因此， 从表格的排版中常常可以看出作者对细节的关注程度。 为了充分展示问题， 我选择讨论一个带有竖线的表格。 带有竖线的表格在 TeX 里较难处理 （但它在 Microsoft Word 里出乎意料地容易）， 虽然这种样式越来越不流行， 且不被推荐。 ¹

2013 年的《通用规范汉字表》是目前简体中文字形的最新标准。其中有若干字为新的类推简化字，如字典末尾均有的「𬭊dù」「𬭳xǐ」「𬭛bō」「𬭶hēi」「鿏mài」（105–109号元素名）。

除「鿏」外，其余均位于 Unicode 8.0 新增的 Ext-E 扩展分区内。在较新的操作系统上，安装有相应的字体，这些汉字均可正常显示。可能并非所有输入法均能输入这些字。（可以根据上面给出的拼音测试一下自己的输入法是否符合国家标准。）

Ext-E 的范围是2B820–2CEAF。使用UTF-8或GB18030编码均需4个字节：

Go 的 fmt 包提供了类似 C 标准库中的 scanf 和 printf 的系列输入输出函数。

// 输入 N*N 矩阵
var G [N][N]int
for i := 0; i < N; i++ {
	for j := 0; j < N; j++ {
		fmt.Scan(&G[i][j])
	}
}

但是 C 的标准输入输出默认是带缓冲的， 而 Go 的不带。 当有大量 I/O 时， 效率较低。 解决的办法是用 bufio 中带缓冲的类型。

in := bufio.NewReader(os.Stdin)
for i := 0; i < N; i++ {
	for j := 0; j < N; j++ {
		fmt.Fscan(in, &G[i][j])
	}
}

同理， 可用 bufio.Writer 对输出进行缓冲， 但是记得在程序退出前调用 Flush() 清空缓冲区。

我手头有一些 jpg 格式的图像文件。 我想把他们打印成 A5 尺寸的小册子。 如果打印机附带了将图像打印成小册子的功能， 那么直接使用即可。 否则， 比较方便的办法是将 jpg 汇集在一个 PDF 文件中， 拼版后交给打印机进行打印。

拼版之前需要确保每个页面的大小为 148mm x 210mm。 对于 300dpi 的图像而言， 即为 1748 x 2480。¹ 可以使用 ImageMagick 对图像进行缩放：

$ magick img.jpg -set density 300   \
                 -resize 1748x2480  \
                 -unsharp 0x5+0.3+0 \
         img-300dpi.jpg

其中， -unsharp 选项用于对缩放后的图像进行钝化遮罩 (Unsharp Mask) 处理， 简单地说就是锐化图像， 抵消缩放所产生的模糊感。

使用 Acrobat 软件可以将若干张图像合成为单个 PDF。

观察一下小册子的印刷方式。 每张纸上印刷的页面并不是按照顺序排列的。 例如， 对于一份 8 页的小册子， 第一张纸正面印的是第 8 页和第 1 页， 反面印的是第 2 页和第 7 页； 第二张纸正面印的是第 6 页和第 3 页， 反面印的是第 4 页和第 5 页。 这样，将这两张纸叠在一起， 第 1 页的反面是第 2 页， 第 2 页和第 3 页恰好相对， 等等。 将所有纸张叠好， 并在中间装订， 然后对折，就构成了一本小册子。

对于上述的小册子， Acrobat 可以直接打印出来。 打开合成的 PDF 文件并按 “打印”， 在打印对话框中选择 “小册子”， 即可。

如果要用 A4 纸制作 A6 大小的小册子， 那么一张纸上需要拼 8 个版面。 仍以 8 页的小册子为例， 这时只需一张纸即可： 正面布置的版面为 \({5;4 \atop 8;1}\)， 反面布置的版面为 \({3;6 \atop 2;7}\)。 将这张纸正面朝外对折， 则反面的第 2、 3 页相对， 第 6、 7 页相对。 用一把裁纸刀沿着折痕将纸裁开， 保持对折时页面的相对位置， 然后令第 1、 8 页朝外， 将两个叠好的半张纸再次对折， 在折痕处装订， 就构成了小册子。