今天做了几件杂活：
更新Highlight.js到8.6。手动更新似乎是很无聊的工作，如果像MathJax那样提供一个latest链接的话就不需要更新了。 更新Hugo到0.14。这个版本的Hugo deprecate了.BaseUrl，并且和我正在使用的主题不能兼容。 本站使用的主题Fork自chibicode/hugo-theme-shiori 。因为更新了Hugo之后不能正常工作，所以我开始自己修改这个主题。其实之前我就改正过Archive页面中的一个逻辑错误，但是我是放在本地的override中的，而没有修改主题本身。这次需要大量的改动，所以干脆修改主题。
转念一想，该主题既然托管在GitHub上，我可以把它做成Pull Request。我以前从来没有做过Pull Request，今天算是实践了一次。
首先在GitHub中点击Fork按钮，几秒钟后，一个本地仓库(repository)就建好了。
接下来要做的就是在本机克隆仓库，设置好远程仓库 upstream ，然后创建一个新的分支。
$ git clone https://github.com/z-rui/hugo-theme-shiori.git
$ git remote add upstream https://github.com/chibicode/hugo-theme-shiori.git
$ git checkout -b patch
upstream 仓库是被fork的仓库，如果原作者修改了代码，那么我只需要pull upstream就可以及时跟上进度。
然后就是修改其中的内容。修改好了以后提交(commit)，然后推送(push)到自己的仓库中。
推送完毕后，在我的GitHub页面上就可以看到生成Pull Request的提示。于是我提交了人生中的第一份Pull Request 。
我在操作过程中学到了一些知识：
不要在master分支中修改代码。如果这样，则GitHub界面上就没有非常显眼的生成Pull Request的提示。尽管仍然可以生成Pull Request，在master分支中修改代码的主要问题是会带来冲突(conflict)。 每次push的时候git都会请求我输入用户名和密码，在反复push的时候显得很恼人。可以打开git的缓存功能，在全局设置中设置credential.helper=cache，就可以只输入一次用户名和密码。 更新: git缓存用户名和密码的功能在Windows上并不好用，因为它依赖UNIX文件系统权限。使用git-credential-winstore 项目可以让Windows凭据管理器保管git用户名和密码。下载git-credential-winstore.exe并复制到合适的目录中，在git的全局设置中设置credential.helper=winstore即可。
继续阅读 → 最近虽然写SQLite图形前端的计划还没有什么进展，但是准备工作已经做起来了。在这过程中常常有意外收获。
在计划使用IUP作为图形界面库的时候，因为LED使用的机制过老，而Lua绑定又要增加新的依赖。（我的经验是，一旦用了IUP的Lua绑定，就会不知不觉地把和GUI不相关的逻辑代码写在Lua里。）所以我打算自己写一个新的GUI代码生成器。它的特点是：
使用IUP的新接口，例如IupSetCallback, IupSetAttributeHandle。 不使用IupSetHandle给每个IUP对象绑定一个全局名称。 生成纯C代码，不依赖Lua。 目前这个项目已经托管在GitHub ，仍在开发中。最新的master分支已经基本能用。
写这个程序其实就是发明一个小型的专用语言，所以免不了和Lex & Yacc这样的元老打交道。最初我打算手写词法分析器和语法分析器，然而只有词法分析器被我手写出来。语法分析器我用Lemon 生成。Lemon和Yacc的语法并不兼容，但好在前者是公有领域内的软件，编译起来也很方便。
Lemon生成的是LALR(1)语法分析器，对语法似乎有很大的限制，总之并不能像我想象地那样好地工作。GNU Bison可以生成更加强大的语法分析器而且和Yacc更加兼容，但我没有尝试。
后来我嫌词法分析器手写也太麻烦，索性用Flex改成自动生成。这就是master分支的最新状态。
很多人把Flex & Bison看成是Lex & Yacc的GNU版本。其实这是不对的。Flex不是GNU系列的软件，采用的也不是GPL协议（而是BSD协议）。所以所谓GNU Flex的称法完全是子虚乌有，但网上一查却还能查出一大堆。（但Bison的确是GNU软件。）
Flex对于喜欢瞎搞编译器的我来说应该是非常趁手的工具。我只需要给出词法定义，所有其他的辅助代码（输入输出、内存管理）全都由Flex搞定。最后程序的主体部分就只有：
do {
token = yylex();
Parse(parser, token, strdup(yytext));
} while (token);
词法分析每读一个记号，就送给语法分析器，如此循环直到文件结束。
值得注意的细节是，yytext不能直接传送给语法分析器。这是因为LALR语法分析器和词法分析器不是同步工作的，读入一个记号以后往往不会立即进行归约(reduce)。等到归约的时候，相应的动作代码才被执行。这时候yytext的内容恐怕已经发生了变化。所以在传送词法记号的时候，就应该传送一份拷贝。
下面说说re2c。re2c是一个相对小众的工具，文档也不多。它可以把DFA（有限状态自动机，词法分析的核心理论）直接编码成(含有很多goto的)C代码。Flex的做法是把状态和跳转规则保存在静态数组里，而其他部分的代码都是同样的模板。
re2c也可以用来写词法分析器。据称，直接编码的DFA构造的词法分析器和手写的词法分析器的效率是接近的，而比Flex那样表格驱动的快很多倍。不过，Flex名字本身意思就是Fast lex，所以究竟能快多少呢？我很好奇。和Flex不同，re2c不产生辅助代码。为了方便起见，我只好采取把输入文件一次性全部读入内存的办法。这样做其实很实用。（Lemon自身分析语法规则的时候，就采用这样的做法。）
我为GUI代码生成器的项目创建了一个新的分支，用re2c 生成词法分析器。
最后说说re2c的补丁。re2c的词法规则是放在形如/*!re2c ... */的注释块中的。据说也可以使用%{ ... %}作为界限符，但是我试了一下，Segmentation fault。
就我个人的审美而言，我觉得%{ %}作为界限符更加美观一点。把有意义的代码写在注释里边是很讨厌的事情。如果要专门为re2c编写语法高亮规则，采用%{ %}这样的界限符也更容易实现一些。
崩溃的原因是re2c自己的词法分析器写的不对，里边有一个硬编码的字符串长度，只适用于前一种形式。补丁 已提交到SourceForge。
更新: re2c的维护者者说他看出了问题，但并不能重现re2c崩溃的现象。真是奇怪啊，在我这里凡是含有%{ %}界限符的文件统统都会崩溃。
更新#2: re2c的维护者很快就发布了re2c的新版本 修正了这个错误。不过他扩展了我提供的补丁，因为程序中还有其他几处类似的错误。
继续阅读 → 我正计划编写一个SQLite的图形前端 。为此我选择IUP 作为图形界面库。
IUP具有如下特点符合我的口味，因此被我选作图形界面库：
C语言接口。GUI常用面向对象的方法处理，所以使用C++的图形界面库更常见。IUP使用C语言实现了一套类型系统，并提供了非常简洁的C语言接口。 跨平台。使用IUP编写的图形界面程序可以运行在Windows和UNIX操作系统上。 相对GTK+、Qt等大型的图形界面库(Qt应该算作综合工具箱)，体积小巧便于发布，配置起来也比较容易。 控件虽然没有其他工具箱来得丰富，但基本够用。文档比较详细。 IUP目前最新的版本是3.14。它仍然存在一些问题，所以我在这里给出两个补丁。
第一个问题是IupSplit中嵌入的IupMatrix有时候会崩溃。我向IUP的作者反映了这个问题。作者回复说他已经在SVN中修复。所以，IUP的下一个版本中将不会再有这个问题。
补丁：（来自SVN ）
--- a/srccontrols/matrix/iupmat_edit.c
+++ b/srccontrols/matrix/iupmat_edit.c
@@ -678,6 +678,7 @@
IupSetAttribute(ih->data->texth, "VISIBLE", "NO");
IupSetAttribute(ih->data->texth, "ACTIVE", "NO");
+ IupSetAttribute(ih->data->texth, "FLOATING", "IGNORE");
/******** DROPDOWN *************/
@@ -696,4 +697,5 @@
IupSetAttribute(ih->data->droph, "VISIBLE", "NO");
IupSetAttribute(ih->data->droph, "ACTIVE", "NO");
-}
+ IupSetAttribute(ih->data->droph, "FLOATING", "IGNORE");
+}
(注：截至写本文时，本站用于语法高亮的脚本Highlight.js 的版本为8.5，它似乎不能正确显示上述代码：最后一部分被作为注释处理了。)
第二个问题是IupTree控件的NAME属性不起作用。即，无法使用IupGetDialogChild找到相应的控件。这是出于兼容性考虑，IupTree控件的NAME属性默认为是TITLE属性的同义词。
IUP的下一个版本也许还会保留这个行为，但我并不需要它。所以我也许应该修改IUP的代码，取消掉这样的兼容行为。要修改这个行为，需要修改平台相关的驱动代码。因为我目前在Windows下开发，所以我只修改了Windows相关的文件。其他平台做类似修改即可。
--- a/src/win/iupwin_tree.c
+++ b/src/win/iupwin_tree.c
@@ -3060,7 +3060,6 @@
iupClassRegisterAttributeId(ic, "KIND", winTreeGetKindAttrib, NULL, IUPAF_READONLY|IUPAF_NO_INHERIT);
iupClassRegisterAttributeId(ic, "PARENT", winTreeGetParentAttrib, NULL, IUPAF_READONLY|IUPAF_NO_INHERIT);
- iupClassRegisterAttributeId(ic, "NAME", winTreeGetTitleAttrib, winTreeSetTitleAttrib, IUPAF_NO_INHERIT);
iupClassRegisterAttributeId(ic, "CHILDCOUNT", winTreeGetChildCountAttrib, NULL, IUPAF_READONLY|IUPAF_NO_INHERIT);
iupClassRegisterAttributeId(ic, "COLOR", winTreeGetColorAttrib, winTreeSetColorAttrib, IUPAF_NO_INHERIT);
我不是很确定修改IUP的源码以使它符合我的需求是不是明智的选择。
一旦修改了IUP的源码，那么基本上来说，我应该将IUP静态链接到我的程序中。因为编译出一个修改过的动态链接库似乎并没有什么意义（不能被其他程序共用）。
还有一种做法是绕过IUP现在提供的IupGetDialogChild机制，另外建立一套获取窗体中的控件的机制。IUP传统的机制是为每一个控件指定一个全局的标识符。像IupSetAtt这样的便捷函数就是在鼓励使用这样的机制（也是为了兼容旧的LED窗体描述机制）。这种做法固然简单有效，但我觉得很丑陋。只可惜像IupTree这样的控件出于兼容性考虑还不能支持NAME属性。
我认为每个窗体有一个单独的名字空间才是正确的做法。不知道是不是出于同样的观点，IUP现在提供了一套新的机制，就是使用控件的NAME属性。这样，控件的标识符的作用域就仅限于其所在的窗体。使用IupGetDialogChild(dlg, "NAME")这样的函数调用来获得dlg窗体中标识符为NAME的控件。
继续阅读 → 这是一道来自高中数学的几何题。值得纪念一下，因为它有好几种证明的办法。有的办法简单，有的办法麻烦。
问题是这样的：如图，矩形的边长\(AB=a, BC=b\)，而\(P\)是\(CD\)上的动点。问：\(\angle APB\)什么时候最大？并说明理由。
根据直觉可知，当\(P\)是\(CD\)的中点的时候，\(\angle APB\)应该最大。
直觉虽然有重要的提示作用，但是有时也不很可靠，所以并不能作为推理的依据。现在让我们忘记直觉，按照一般的分析办法来处理这个问题。
继续阅读 → SQLite3非常与众不同 。它的类型系统也不同于大部分的数据库管理系统(DBMS)。
通常，DBMS使用静态类型(static typing)，即数据表的每一列中只能存放同一种类型的数据，这个类型在创建表的时候就已经确定。而SQLite3使用称为manifest typing的类型系统，它允许每一列中存放不同类型的元素，实际上很像动态类型。Manifest typing的准确译法我不知道。按照字面意思可以翻译成“显式类型”，可是这又无法体现它动态类型的特点。
注：有的教材把行称为“记录”，把列称为“字段”。我认为这些名字并不形象，对理解数据表帮助不大。
首先，数据表的每一列并没有严格的数据类型，只有具体的数据有类型。SQLite3的数据类型有5种，如下面的例子所示。
SELECT
TYPEOF(NULL),
TYPEOF(-9223372036854775808),
TYPEOF(1e-5),
TYPEOF('hello, world'),
TYPEOF(X'DEADBEEF');
--> null|integer|real|text|blob
虽然和静态类型有很大的不同，但是实际使用的时候，SQLite3和使用静态类型的DBMS是兼容的。
CREATE TABLE BOOKS(
ID INTEGER PRIMARY KEY,
NAME VARCHAR(255),
PRICE REAL
);
INSERT INTO BOOKS(NAME, PRICE) VALUES
('The Art of Computer Programming', 259.99),
('Concrete Mathematics', 57.57);
你照样可以在创建表格的时候指定各个列的类型，不过它们只是一个摆设，并不会被SQLite3严格执行（有一些例外，见下文）。事实上，SQLite3中根本没有VARCHAR(255)这个数据类型，你可以指定任意名称的数据类型。这样做实际上提高了SQLite3和其他DBMS的兼容性。
继续阅读 → 前天玩了一次别人的三阶魔方，5分钟内都没能复原。
岁月不饶人，说的也不是没有道理。
想当年我也曾凭借一个简化版的CFOP公式，在1分钟内就能把三阶魔方复原。（当时的世界纪录是6.x秒。我当然差的还远，即便要自称“高手”，也必须是30秒以内复原才算；但是在同龄人之间自然可以炫耀一番。）5~6年的时间，竟然已经几乎忘光了。
想想也可笑。“想当年”，我们不也是猛练各种解题技巧，在100分钟内把一张数学卷子给做完？5~6年以后，就算不设时间限制，恐怕有些题也是没法做出来。这么说起来，当初又为什么要训练到那样的程度呢？
不过魔方确实是一个很有意思的玩具。就算我练不成速拧高手（现在的世界纪录大概是5.x秒，时代在进步），没事玩玩也是挺有意思的。所以产生了重拾三阶魔方的念头。
我买了一只型号叫作GAN357的魔方，它附送了一份公式参考，包括入门级别的层先法和比较高级的CFOP法。层先法总共10个公式，比较适合入门。对于拼底块十字这种最最基础的没有公式可言的操作，参考上也做了详细的解释。所以，仅靠这张参考就完全学会魔方复原，一点也不困难。CFOP法是层先法的改进，提高了复原的速度，但是相应地，公式也就大大增加，多达119个公式。要熟练掌握CFOP是不那么容易的，但是一旦熟练，复原魔方的时间就可以缩短到30秒乃至更短。
应该说，现在玩魔方比我当年要轻松多了，魔方买到手攻略也就送到家，还有“玩”的必要吗？直接就是入门到进阶一条龙服务，把菜鸟培养成高手。
我当年玩魔方的时候哪有攻略可查。可惜，凭借自己的智慧没能复原整个魔方。最好的成绩是复原了前两层，而对于第三层根本束手无策（其实是不舍得破坏前两层已经拼好的所谓“完美”状态）。
出于想要复原魔方的强烈愿望，还是忍不住去网上查找复原魔方有没有什么窍门。然后就接触到了所谓的层先法解法和公式记号。对于公式，心里只能用“神奇”来评价；它就像巫师的咒语一样，念一遍就会起效果。按部就班地操作，最后果不其然复原了整个魔方的全部六面。当时的心情，我想每个玩过魔方的人都有切身体验吧。
我曾把复原魔方的公式记在了一本笔记本上。那本笔记本后来在一次清理房间的过程中被意外地和废纸一起卖掉了，就再也找不到了。
但我想，要不是一开始有过自己的动手和研究，而是上来就套公式的话，复原一个魔方就应该是意料之中的理所当然的事情，恐怕不会有太多的新鲜感和成就感。如果一定要类比的话，应试教育就是那种一上来就把所有招式都教给你，解题只需套公式而无需深入研究和理解，入门到进阶的一条龙服务，把门外汉直接培养成解题能手。如果一个人志在获得魔方速拧的世界冠军，那么我觉得“一条龙服务”不失为一种实际的选择。但这同时意味着失去了所有的乐趣和成就。死记硬背+苦练不说，所有的成就都也不过是前人的成果，我做得再好，只能说明我和前人一样好，否则就是我连前人也不如。
并非每个人生下来都有想取得速拧冠军的理想。真正有这样理想的人，一般来说，一定是玩了很长时间的魔方，对它有很深的兴趣的人。在此基础之上，他才愿意去记忆大量的公式并且训练手速。对玩魔方不感兴趣的人，或者天生手笨的人，即便有“一条龙服务”摆在面前，也不见得会动心。不幸的是，每个人生下来就被寄予考上好学校的期望，因而注定着要参与各种各样的招生考试。选择应试教育其实只是这样的大背景下一种必然的结果而已。
扯远了。我不否认间接经验的价值。事实上，因为间接经验的存在人类的知识才能迅速地发展。虽然原创研究是推动人类进步的重要因素，但现实中大多数人最常用的知识，其实都是很久以前传下来的间接经验（加减乘除？）。有的人手快，有的人脑子好。脑子好的人想出了速拧的公式，但他未必能创造世界纪录。手快的人可能没法自己推导出魔方的复原公式，但是他通过理解他人总结的公式，发挥自己手快的特长，就能创造世界纪录。闻道有先后，术业有专攻，如是而已。
正因为公式的存在，魔方才可能成为大众的玩具。复原三阶魔方其实是一种在外行人看来非常了不起，但其实很容易的本事。不少人学复原魔方的初衷只是为了炫耀。炫耀炫耀也就罢了，不宜以此宣称自己天资聪颖，最多也只是熟能生巧罢了。
刚才试了试，似乎仍然需要1分多钟的时间才能复原。这样的成绩似乎还差得很远，不过我并不在意。自己玩得开心就好。
今天我另外还看了三阶魔方的其他解法（不是基于层先法），看的时候甚感吃力。感觉层先法在我脑中已形成固定模式无法改变。这大概也是很多其他领域中会出现的事情：一旦对某种理论高度熟悉，就会形成固定的看法，而所有其他的理论都会被看作荒诞之谈。
继续阅读 → 今天我做了两件事，其一是了解了样条插值的概念，其二是观察了使用有限差分方法求解的调和场。做这两件事都用到了gnuplot。
Gnuplot 是一个可用于作图的免费软件。使用它可以将数值计算的结果以图像的方式呈现，以获得直观的感受。
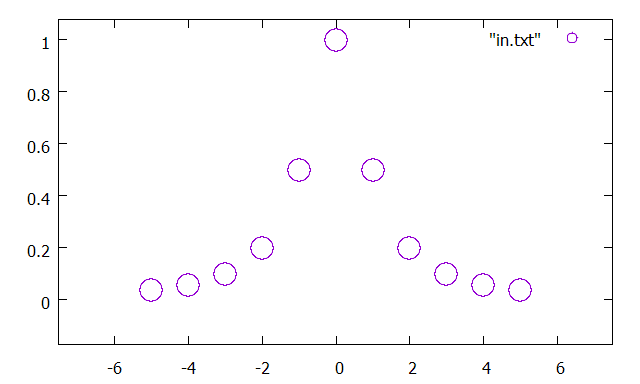
观察插值函数 试想原本有一个连续函数，由于测量的原因现在只知道其中的个别点的位置。
但是我想知道中间某个点处的函数值，我会这么做：用一条光滑的曲线把这些点连接起来，然后根据图像来找到对应的函数值。这就是科学实验中常用的图解法的原理。
继续阅读 → 本定理来自一道算法竞赛题：
给定任意多条边，每条边都是不超过1,000,000,000的正整数。请给出一个算法，判断其中是否存在3条边可以构成三角形。
应用该定理可以有效地解决此问题。
定理 给定n个边长，如果其中最大的边长与最小的边长的比值小于第n个斐波那契数，那么其中必存在3个边长可以构成三角形。
应用 由题中条件可知，最大的边长和最短的边长的比值不超过\(1,000,000,000 < F_{45}\)。所以，只要边的个数达到45，根据上述定理，就必然存在3条边可以构成三角形。如果边的个数少于45个，也很好办，穷举解决即可（\({45 \choose 3} = 14190\)，穷举量很小）。
继续阅读 → Lua 本身已经是一个十分轻量级的脚本语言。在我的64位Windows上编译出来的lua53.dll仅248K。(参照物：python34.dll为3963K。)
Lua Technical Note 1 介绍了通过删减功能来进一步减小Lua的二进制体积的方法。这篇文章针对的是Lua 3.2，16年前的版本，尽管如此，它仍然给了我很大的启发。
首先看Lua 5.3中哪些模块占用的二进制体积最多：
size %all %core file
23571 7% 12% lauxlib.o
20909 6% 11% lparser.o
20256 6% 11% lapi.o
18403 5% 10% lvm.o
14413 4% 8% llex.o
13526 4% 7% lcode.o
12584 4% 7% lgc.o
10214 3% 5% ldebug.o
8967 3% 5% lobject.o
8776 2% 5% ldo.o
7002 2% 4% ltable.o
5087 1% 3% lundump.o
4887 1% 3% lstate.o
3970 1% 2% ltm.o
3832 1% 2% ldump.o
2818 1% 1% lstring.o
2525 1% 1% lfunc.o
2170 1% 1% linit.o
1810 1% 1% lopcodes.o
1498 0% 1% lmem.o
1406 0% 1% lzio.o
860 0% 0% lctype.o
189484 54% 100% (core)
继续阅读 → Lua 在有些地方没有采用其他语言(尤其是C)的约定俗成，所以经常给程序编写者带来惊喜(surprise, “gotcha”)。根据我的经验，整理如下：
不等号是~=，而不是!=。 这是我写Lua程序时最常犯的一个笔误。只能说，几乎所有的程序语言，不等号用的都是!=(C家族)，还有一部分用<>(Pascal, Basic, SQL)。用~=真的只有Lua一家。 继续阅读 → 
